100円から読める!ネット不要!印刷しても読みやすいPDF記事はこちら⇒ いつでもどこでも読める!広告無し!建築学生が学ぶ構造力学のPDF版の学習記事 正方形の面積は? 正方形の面積は、縦×横で求めます。下図の面積であれば、辺の長さがaなので A=a×a=a 2 半径がわかれば、すぐに面積もわかります。円の面積の公式を考えて、 $$\text{面積} = \pi r^2 = \pi \times \left( \frac{8}{\pi} \right)^2 = 4$$ となります。面積は4cm 2 です。 これまでの最高記録である正方形の面積(16mc 2)を大きく超えました。 図形のまわりの長さが同じ場合、もっとも面積が大きくなるのは"円" なのです! まとめ(1)正方形PQRSの面積は何cm2ですか。 (2)かげをつけた部分の面積の和は何cm2ですか。 <円とおうぎ形 面積その4> 右の図のように直径が重なった 2つの半円があ ります。小さい半円の中心はAで ,半径は 30cm, 大きい半円の中心はBで ,半径は40cmです。この
円の中の正方形の解答と解説 多目的ルーム 楽天ブログ
円 内接 正方形 面積
円 内接 正方形 面積-解法の見通し 求める面積は左図のχの部分 つまり、正方形から a,b,c,dの4カ所を ひいてやれば良いことが分かる! a,b,c,d は合同なので a の面積だけの求め方を考える! a の部分の面積を求めるには左図の手順でよい! χ=(正方形)-(a+b+c+d)・等円の直径が1cmのとき、正方形1辺の長さを求めてください。 ・斜線部分の面積を求めてください。 ただし、円周率はπとします。 ※嘉永3年(1850)に菅原神社(一関市舞川)に奉納された算額の問題です。 審査員講評 今回も中級問題には、小学4年生から85歳という高齢の方まで、幅広い年齢層




円の面積 円周の長さ わさっきhb
ぜいたく 正方形 円 面積 世界一やさしい 円の面積を求める問題の解き方 働きアリ 正方形と円で囲まれた図形の面積 おわり Takapの数学日記 モンテカルロ法による円の面積計算 円の中の正方形 Math 算数のコツ 18 円の中の正方形 働きアリ 正方形と扇形の面積をつかった問題がわか 第131問 正方形の面積 図形ドリル 45度 6年生 正方形 直角二等辺三角形 ★★☆☆☆☆(小学4〜5年生対象) 思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。図形ドリルでは,色々なタイプの図形問題を取り上げています。 入試解説 6年生 男子校 5年生 正方形 正三角形 東京 兵庫 灘 算数オリンピック 共学校 面積比 円 図形NOTE logix出版 角度 1日目 直角三角形 4年生 女子校 相似 立方体 長方形 おうぎ形 30度 正六角形 16年 17年 19年 トライアル 18年 年 ファイナル 二等辺三角形 直角二等辺三角形 21年 立体の切断 15年 図形の移動 共通部分 大阪 面積の和 12年 13年 3年生 ジュニア
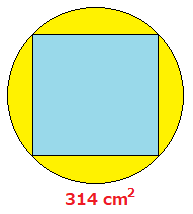
四角形 4角形 面積計算 公式 求め方 正方形 長方形 縦 横 自動 area 面積 四角形 面積; 今日は、中学受験で超頻出の「正方形の中にある正方形の面積」問題を紹介します。 親子で挑戦してみてください! 問題 図のように正方形の中にぴったり円が入ってい円とおうぎ形⑹ 弓形の面積 16 16 次の図は、1辺8㎝の正方形ABCDと、直径8㎝の円を4個組み合 わせた図形です。色のついた部分の面積を求めなさい。ただし円周率 は314とします。
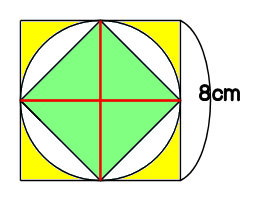
円積問題 えんせきもんだい quadrature of a circle 円の正方形化,すなわち与えられた円と等しい面積の正方形を作図することをいう。 古代においてこの問題は,重要な未解決の作図題と考えられていた。 しかし,与えられた円の周と同じ長さの直線,あるいは与えられた円と同じ面積の正方形を円の中の正方形(基礎) 面積を求めよう 一辺が8cmの正方形の中に、円が接するようにあり、円の中に正方形が接するようにあります。 中の正方形の面積は、何平方センチメートルでしょう。 考え方1 赤い中の正方形の対角線の長さは8cm それなら、8×8で、大きな正方形の面積が出て、 その半分が、中の正方形の面積だ。 大きな正方形を、折り紙をおるように、中に円の面積学習における学習の流れ (子ども の音符の流れ)を次のように考えた。 ① 円の面積は円周内部の面に存在し,円 の半径と依存関係にあることに気づく。 ② 円の面積は,その円の半径を一辺とす る正方形の面積の2倍より大きく4倍よ




面白い数学の問題 半円の中の2つの正方形 証明までが解答です そらの暇つぶしch



あとまあく数学の演習 円の面積小5以上
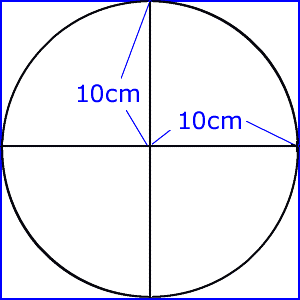
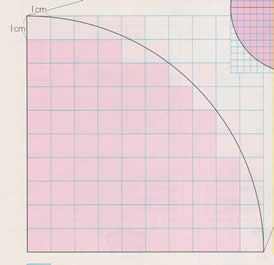
採点する やり直す 解説 3 半径 10 ,中心角が90°の扇形の面積 円の面積の4分の1だから,10 2π ÷4=25 π π 採点する やり直す 解説 4 下の図の灰色で示した図形の面積 扇形の面積は円の4分の1で25 π ,これから三角形の面積 10×10÷2=50 を引く図形の面積の求め方(公式ほか) 正方形・円・長方形・平行四辺形・三角形・扇形・楕円・台形・双曲線・放物線・六角形・多角形 光正株式会社 役立つ資料シリーズ 図形の面積の求め方 A=面積 A=s 2 A=1/2d 2 S= d= d=1414 s=1414 A=面積 =弧の長さ a=角度 A=面積 A=面積 =弧の長さ この部分の面積は以下のように求めます。 この赤いおうぎ形は大きな円の4分の1になっています。 円の半径は正方形の一辺と同じなので1cmです。 従ってこのおうぎ形の面積は1×1×314÷4=0785ですね。 そこからこの青い三角形を引きます。 この青い三角形




円の面積 算数用語集



6年算数 円の面積 1 アニメでわかる教え方
(2) 円の面積は,正方形の面積の157倍だから, 斜線部分の面積は正方形の, 1 57 1 = 0 57 倍。 4 4 0 57 = 9 12(cm 2 ) 答一辺の長さ $a$ の 正方形 (せいほうけい) の面積 $S$ は、次の公式で求められます。 正方形 (せいほうけい) の面積 \begin{align*} S = a^2 \end{align*} 面積 = 一辺 × 一辺正方形の面積 A: 面積: 長方形の面積 A: B: 面積: 円 円 半円 扇形 円周長から面積 四角形 四角形 四角形 4辺と対角線 角パイプ 三角形 三角形 三角形(3辺) 四角形 平行四辺形



円の中の正方形 基礎




斜線部の面積を計算してください これはクイズではありません マジで難 Okwave
5 1 単純な場合 (2次元の面積) ここでは,モンテカルロ法 (Monte Carlo method)呼ばれる乱数を使った一風変わった数値 積分の方法を示す.モンテカルロとは有名なモナコのカジノで,博打をするところである. この方法を少し学習すると,名前の由来が分かった 正方形の面積は80㎠なので、正方形の1辺を ㎝とすると、 × =80 よって、直径×直径=80 すると半径×半径も分かります。 <答え> 直径×直径=80なので、半径×半径=(直径÷2)×(直径÷2)=直径÷4=となります。 よってこの円の面積は×314=628(㎠)三角形の面積 ・正三角形の面積 1辺の長さを指定して、正三角形の面積を計算します。 ・三角形の面積(底辺と高さ) 底辺と高さから三角形の面積を計算します。 ・三角形の面積(2辺と間の角度) 2辺と間の角度から三角形の面積を計算します。



6年算数 円の面積 1 アニメでわかる教え方




解き方わかる方がいたら教えていただきたいです ちなみに答えは32p 64です Clear
円周や弧の長さ、円の面積やおうぎ形の面積は 「円周率の倍数 」です。 円周率が314のこの問題では、 弧の長さ157cmを「5×314」の形に変えておくことができます。 はじめにありました「覚えておきたい」で、 「2×円周率~9×円周率」の値 が頭に入って正八角形の対角線で囲まれた面積 東海中 08 円内を転がる正方形 雙葉中 07・6 転がる正方形 清真学園中 06・後期・3 長方形の通過する部分の面積など ラ・サール中 11・5 辺の通過する部分の面積 灘中 16・第1日・9 転がる正方形 駒場東邦中 16・3314×36= 314×49= 314×64=096 314×81= 正方形や円などの面積を速く正確に計算するために、同じ数をかけた積(二乗・自乗)の計算方法をマスターしましょう。 (参考) → 二乗の速算法 平面図形の面積の基本問題 問題1




円の面積 練習応用 Youtube




円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ
面積の計算 ・ 正三角形の面積 ・ 三角形の面積 (底辺と高さ) ・ 三角形の面積 (2辺と間の角度) ・ 三角形の面積 (1辺と両端の角度) ・ 三角形の面積 (3辺の長さ) ・ 正方形の面積 ・ 長方形の面積 ・ 台形の面積円 正方形 5年生向け 灘中学校1999 相似 台形 5年生向け 東京農業大学第一高等学校中等部 平面図形 no 873 問題と解説 面積 4年生向け 専修大学松戸中学校 平面図形 no 857 問題と解説 四角形abcdは正方形であることから、長さの等しい辺に着目しましょう。 角度 正方形この正三角形の一辺は円の中心点より六角形の各点へと 引かれた線であるため長さはRとなる。 これより三角形の面積は 2 円に内接する六角形の面積はこれを6倍したものである。 円に外接する正六角形も同じ大きさの正三角形を6こ組み合わせたものである。




円の面積 その2 家庭学習レシピ
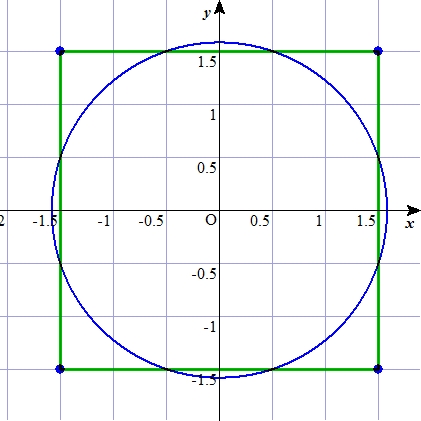



正方形と円の面積 コ コ ロで遊ぶ算数教室
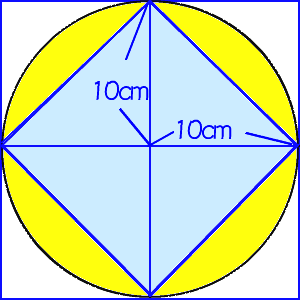
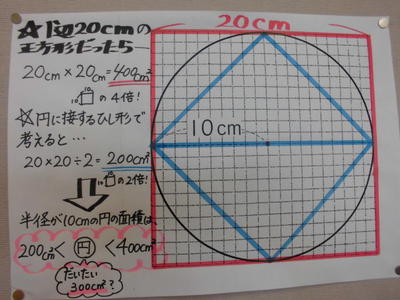
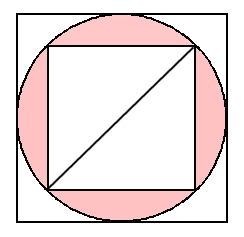
円の面積を求めるためには、まず円の半径を求めなければ ならない。正方形の一辺は円の中心をとおっていないので 直径ではない。この円の面積はこの円の中心をとおる、正 方形の対角線である。すなわち、半径はこの対角線の半分 の長さである。このA=面積 正方形 長方形 平行四辺形 備考 a寸法はb辺に対し直角に測ったもの 直角三角形 a=面積 鋭角三角形 鈍角三角形 台 形 不平行四辺形 なお点線にて示すごとく二つの三角形となし、各々の面積を計算し、 その和をもって不平行四辺形の面積を算出してもよい。 a=面積 正六角形 正八角形 正右の図の四角形ABCDと内側の四角形は正方形です。 内側の正方形の面積が54cm2のとき、正方形ABCDの 面積は何cm2ですか。 解説: 内側の正方形をひし形として考える。 対角線×対角線÷2=50から、 対角線×対角線=100。 内側の正方形の対角線は円の直径でも あるので、四角形ABCDの面積は100cm2。
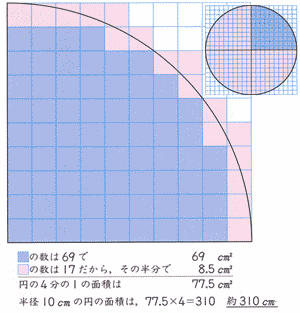



実践記録算数5年



Math 算数のコツ 18 円の中の正方形 働きアリ The 2nd
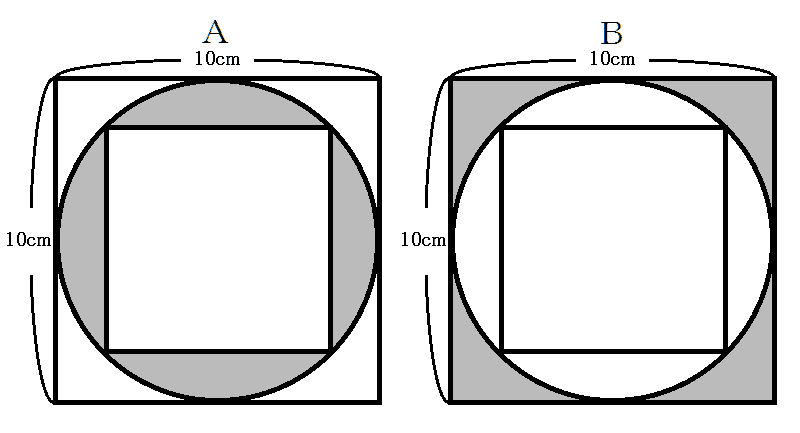
円の外側の正方形の面積は、 (10×10)×4=400 です 半径10cm円は、その内側にあります。 なので、半径10cm円の面積は、 1辺10cmの正方形4つぶんより小さいことをとらえさせます。




超頻出 正方形の中に正方形の面積問題 恋する中高一貫校 適性検査 徹底攻略



円積問題 Wikipedia
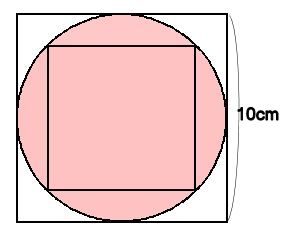



円の中の正方形
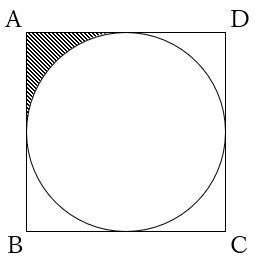



半径の分からない円の面積 中学受験プロ講師ブログ




円と正方形の長さ比べ 香料ゐっすゐの夢



1
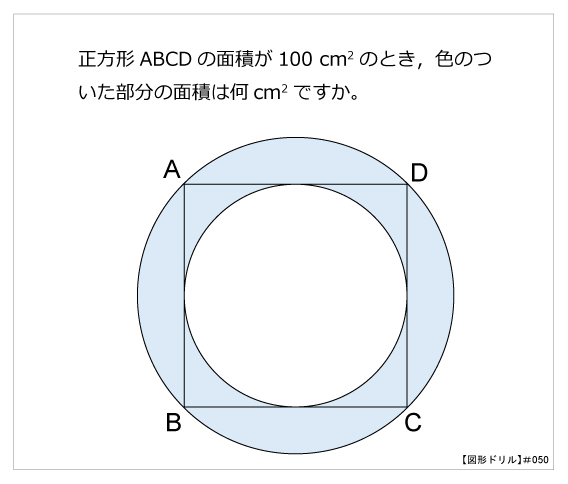



図形ドリル 第50問 内接円と外接円 算数星人のweb問題集 中学受験算数の問題に挑戦




この問題教えてください 1辺がcmの正方形の内側に接している Clear



正方形の面積
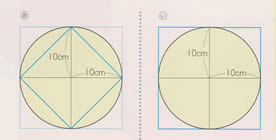



円の面積 1 5
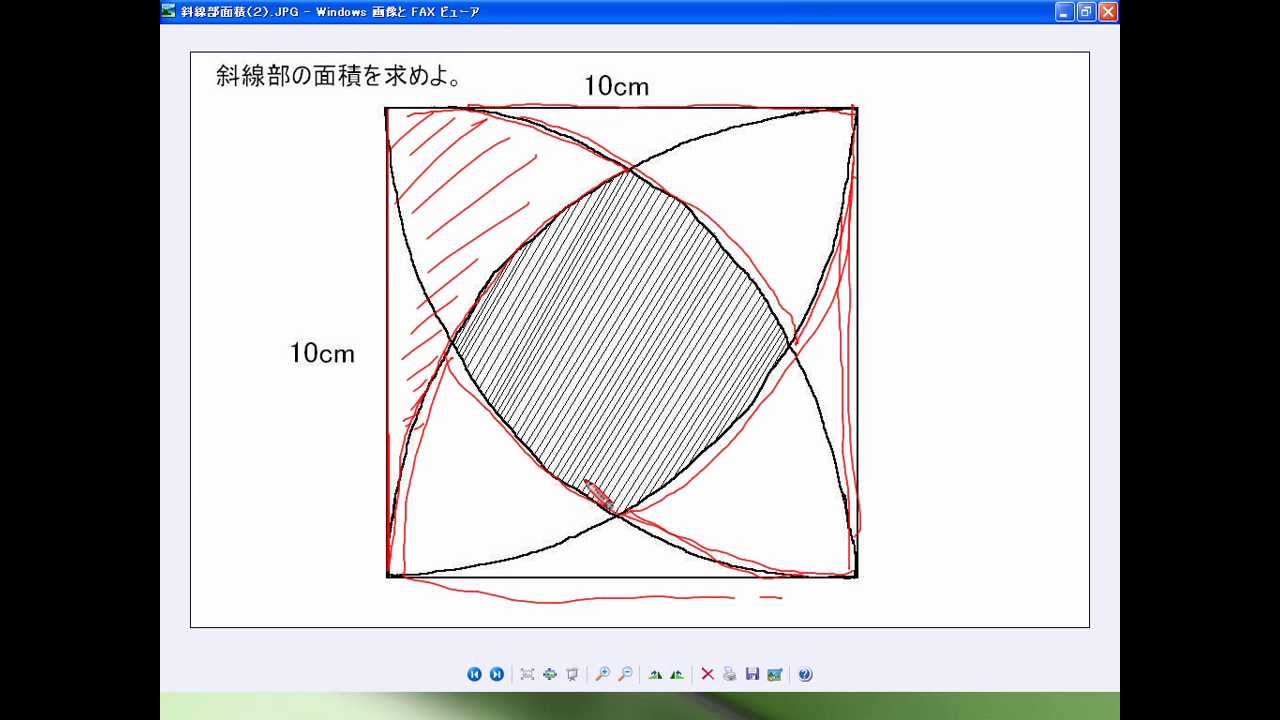



斜線部の面積 4 1辺10cmの正方形の場合 Youtube




半円に内接する2つの正方形の面積の和 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog



頭の体操 図形編




はっぱ型 の図形の面積 身勝手な主張




正方形と円で囲まれた図形の面積 おわり Takapの数学日記
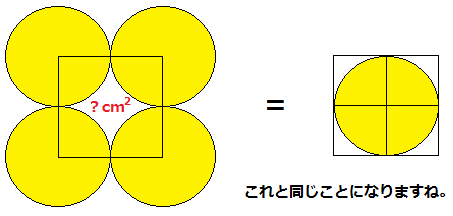



4つの円のすき間の解答と解説 多目的ルーム 楽天ブログ
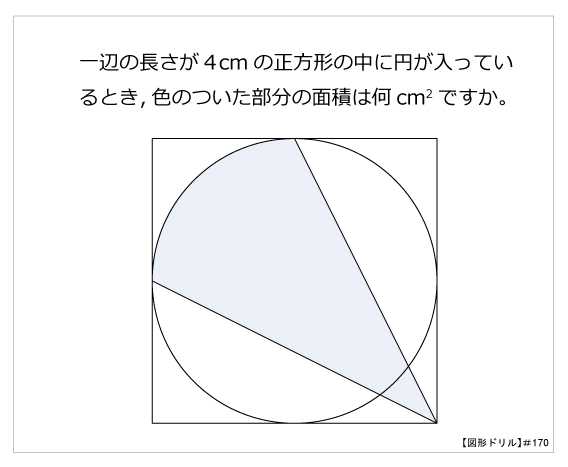



図形ドリル 第170問 円と正方形 算数星人のweb問題集 中学受験算数の問題に挑戦
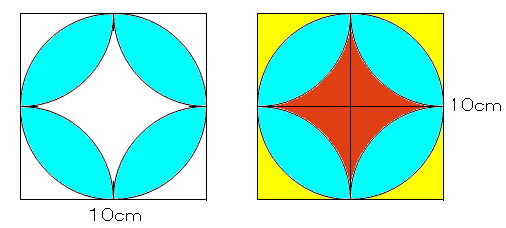



算数 扇形の面積の応用 葉っぱ型図形の面積 なるほどの素
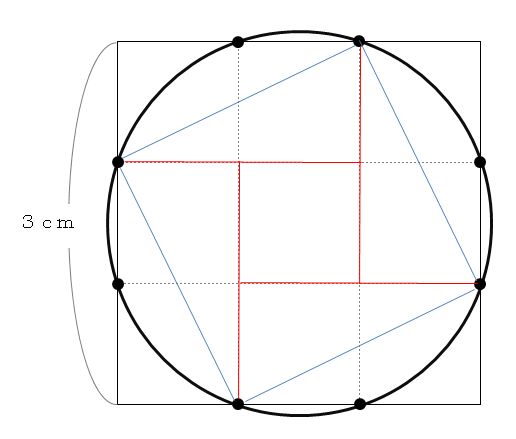



入試に使える算数の基礎 半径 半径



下の図は正方形の中に四分円と 半円を2つかいたものです 斜線部分の Yahoo 知恵袋



Pronity 57 球の直径 円周 面積 体積に合わせた 正四面体 正三角形と立方体 正方形の比例



1
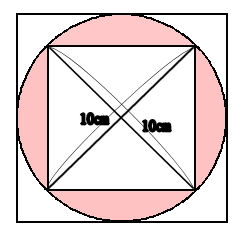



円の中の正方形
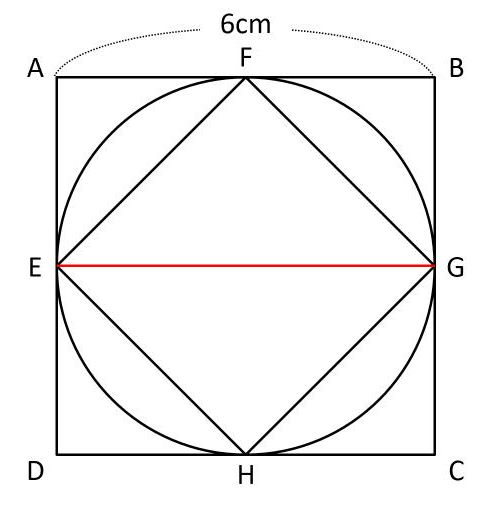



正方形の対角線の長さを求めたい 小学生が算数の知識を使ってどこまでできる 中学受験ナビ



正方形から円を引いた面積 灘中学 2007年 これが中学入試に出た図形問題



求積問題 正方形と扇形



正方形とおうぎ形 奈良学園中学 算数入試問題 1998年 どう解く 中学受験算数



円の面積 面白ゼミナール
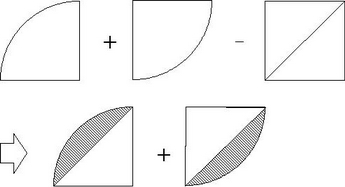



0 57の暗記 を活用しよう 前田昌宏の中学受験が楽しくなる算数塾



正方形に円が重なる面積の問題です 正方形に 正方形の一辺を半径と 数学 教えて Goo




名寄 算数数学教室 前回問題の解答です 円の中にピッタリ入る正方形に 対角線を2本書いて考えます Facebook



ビュフォンの針実験 針を投げるだけで円周率が求まる 数学の面白いこと 役に立つことをまとめたサイト



三石 数学塾 円の面積




円の中の正方形の解答と解説 多目的ルーム 楽天ブログ



円積問題
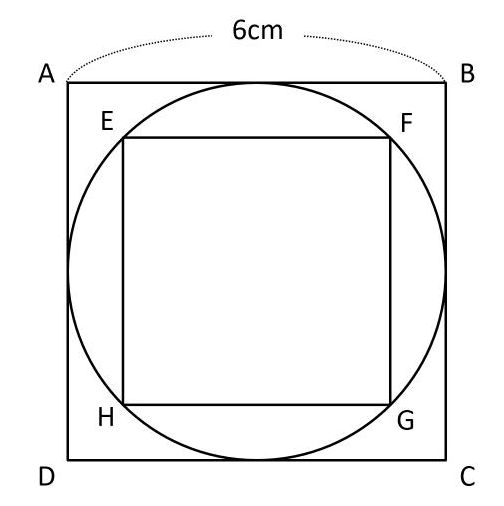



正方形の対角線の長さを求めたい 小学生が算数の知識を使ってどこまでできる 中学受験ナビ




Mondai55




平成27年度算数教科書読み比べ 8 円の面積の求め方 わさっきhb
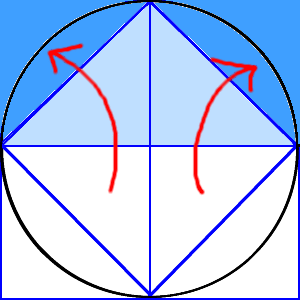



6年算数 円の面積 1 アニメでわかる教え方



小学生向け難問その 2 解答 途中まで While Im Automaton



いわき市 全校表示 へ いわき小中学校ホームページ



正方形の中に四分円を2つ書いたもの 影の部分のまわりの長さはcm とい Yahoo 知恵袋




正方形と扇形の面積をつかった問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく
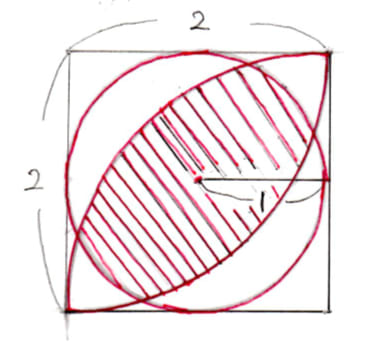



数学難問 正方形と円弧で囲まれた図形1 Takapの数学日記
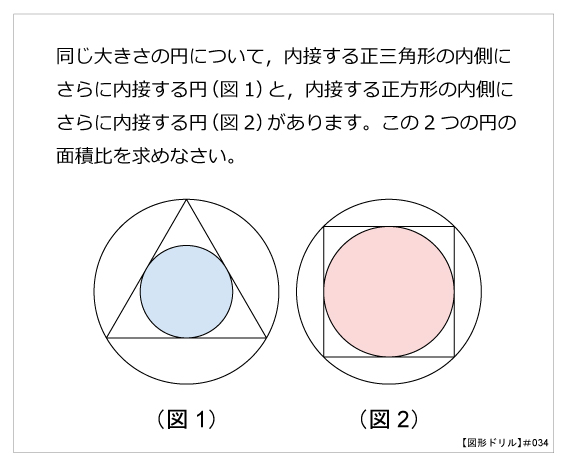



図形ドリル 第34問 内接円の面積比 算数星人のweb問題集 中学受験算数の問題に挑戦




円の面積 円周の長さ わさっきhb



円の面積の求め方についてです 正方形のなかに直径9cmの円があ Yahoo 知恵袋




Twitterで拾った問題 半円に接する2つの正方形 オンライン講師ブログ
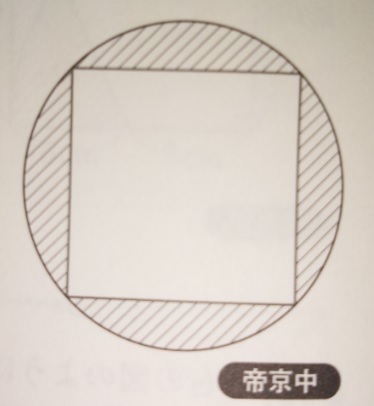



円と正方形で覚えるルールはこの2つ 中学受験 塾なし の勉強法



正方形内の円 開智中学 2010年 どう解く 中学受験算数



1
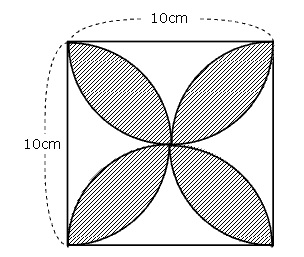



おうぎ形の面積の求め方2つと葉っぱ レンズ 形の面積の求め方3つ 等積移動 中学受験 塾なし の勉強法
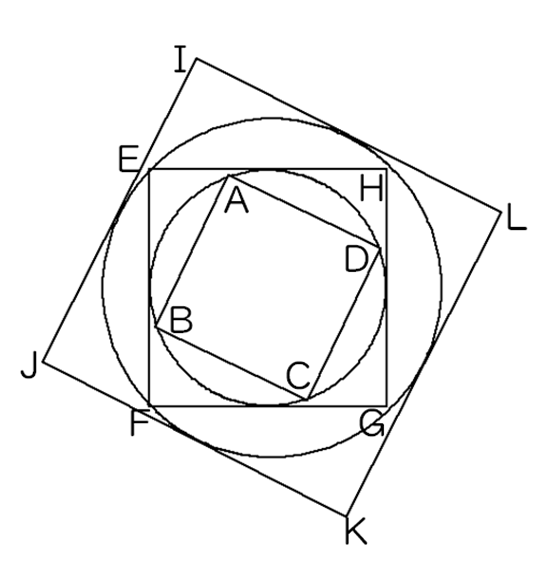



円と接する正方形の面積 女子学院 H16大問2の4




Sapix サピックス 4年 みんな知らない 円の面積 正方形 3 14 です たぶお Sapix サピックス A1 養成講座



正方形と円 2015年 開成中学の面積問題から 図で解く算数



この画像のように 一辺の長さが10センチの正方形がピッタリ入る円の Yahoo 知恵袋




長女の中学受験 算数の復習で最低限覚えておきたい図形 円と正方形の話を復習しました Pi Sukeのネットな生活



求積問題 正方形と扇形
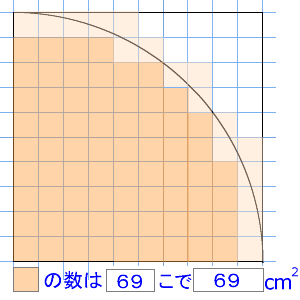



6年算数 円の面積 1 アニメでわかる教え方




中学受験算数 豊島岡女子学園中学校 10年 正方形の辺を三等分した点を通る円の面積を求める問題 Youtube




収納量の比較 数学の先生が 四角と丸の収納力を計算したら 中学受験から大学受験の塾プリント整理専門 プロ家庭教師 整理収納アドバイザー中島亜季 大阪京都奈良




4つの円のすき間の解答と解説 多目的ルーム 楽天ブログ



Www Pref Fukushima Lg Jp Uploaded Attachment Pdf
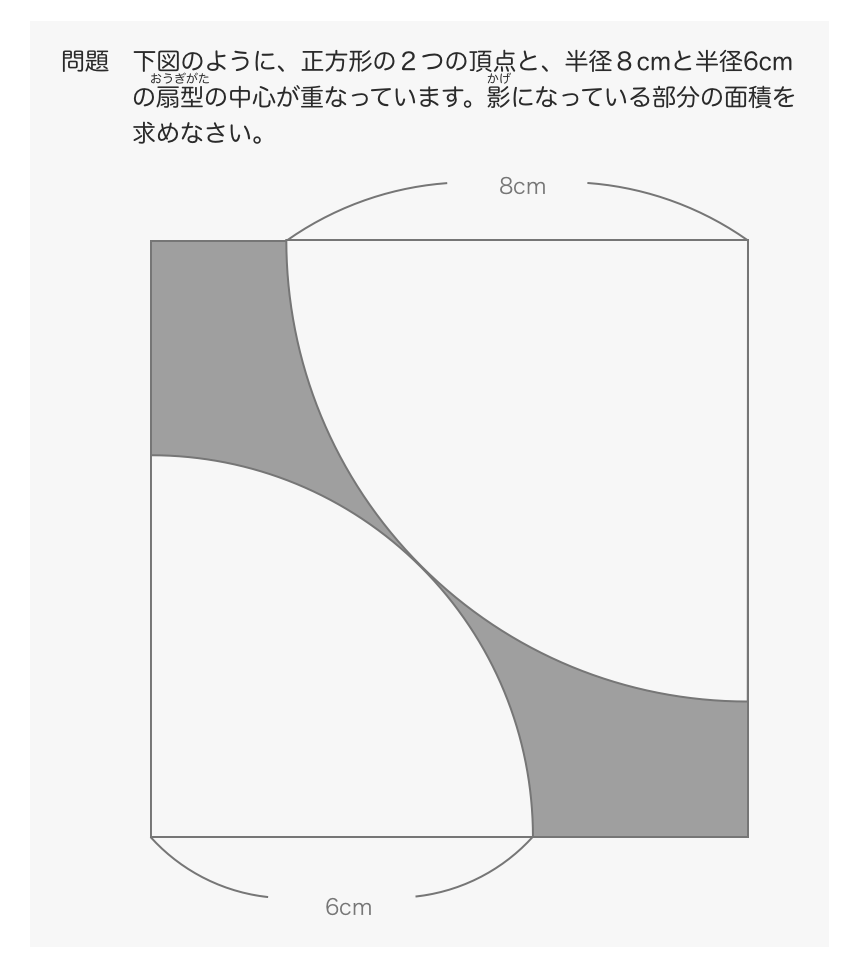



自作教材 円と扇形2 本質と技とコツ カテキョウブログ




面積の求め方 算数の教え上手 学びの場 Com
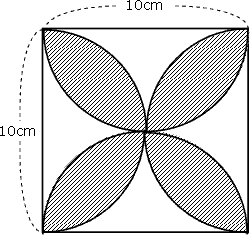



面積の求め方 算数の教え上手 学びの場 Com




朝日新聞デジタル 円の面積 正方形を使って考えよう 山上浩二郎の大学取れたて便 大学 教育
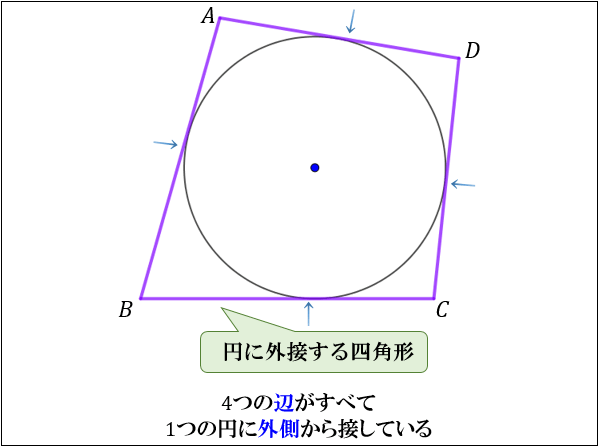



円に外接する四角形の性質まとめ 向かい合った辺の合計が等しくなる理由 アタリマエ




15年度 愛光中学校 算数 1 6 面積



半径5cmの円の中に 下のような 正方形をかきました この正方形の 面積は何cmですか




標準 おうぎ形と正方形の面積 なかけんの数学ノート
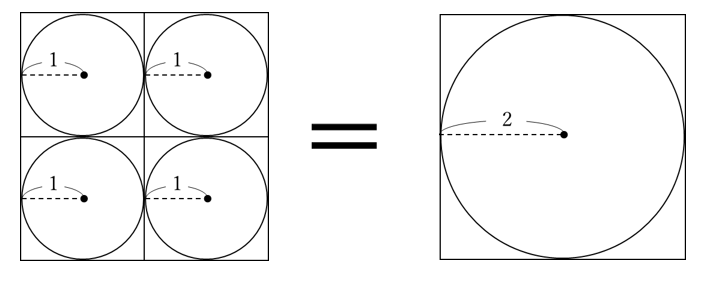



円の相似を利用した面積の計算 中学受験プロ講師ブログ




正方形と扇形の面積をつかった問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく
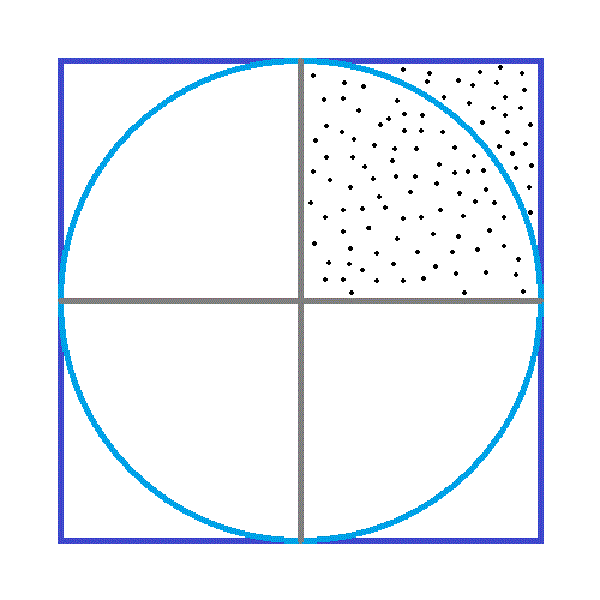



モンテカルロ法による円の面積計算



静岡県立 沼津市立 共通 18算数 図形の面積 中高一貫 適性検査解説 Note



雑学のソムリエ 円の面積を直径で表す



円の面積 2 5



図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト



数学ナビゲーター掲示板 One Topic All View Re 1 正方形に内接する円と四分円の共通部分の面積 Page 0



円の中の正方形



円の面積 面白ゼミナール



Q Tbn And9gct8mjpenhvsxxfek Ceorhkk1e5jnkqcmelwl1yafnkyt4mflap Usqp Cau
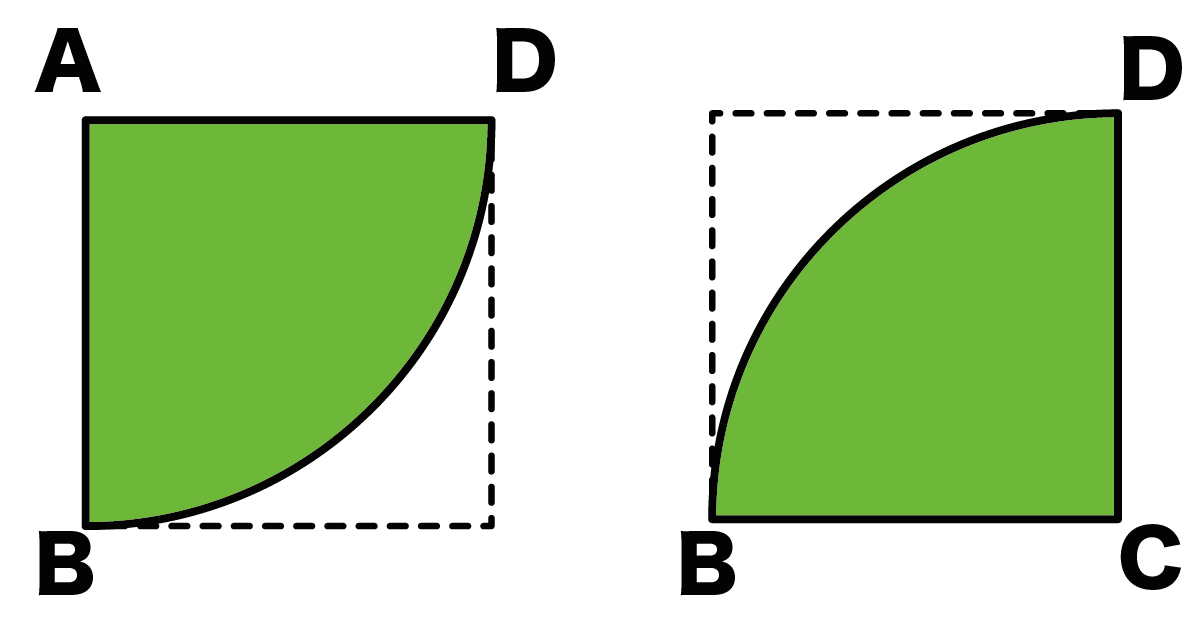



正方形と扇形の面積をつかった問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく
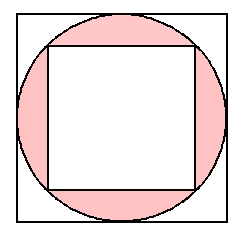



円の中の正方形




正方形に内接する円と四分円に囲まれる面積 高校時代に友人から聞いて解けな Okwave
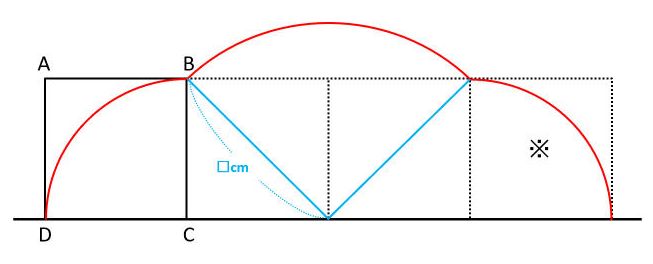



正方形の対角線の長さを求めたい 小学生が算数の知識を使ってどこまでできる 中学受験ナビ



No 086 巻頭言 半径は計算せずに円の面積を求める Fumiononaka Com Newsletter




06年5月問題解答例
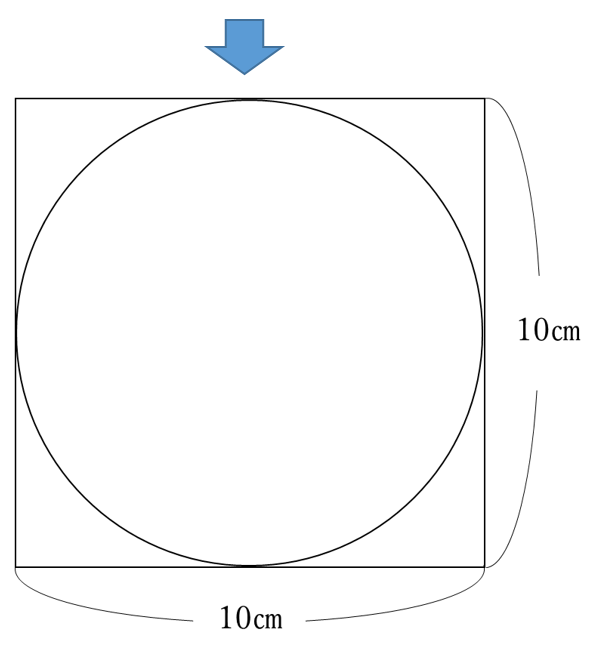



円の相似を利用した面積の計算 中学受験プロ講師ブログ
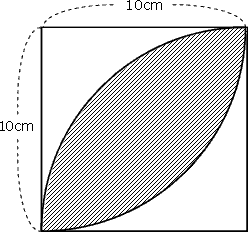



面積の求め方 算数の教え上手 学びの場 Com



0 件のコメント:
コメントを投稿