になってるよ。 この2つの三角形の面積比をだしてみよう! 公式なら2ステップで面積比だせちゃうんだ。 相似比を求める;次の図の ABCと ADEのように,1つの角(∠A)が共有されている2つの三角形の面積比について考えます。 ABC ABE=CAEA=bd(=abad)① ABE ADE=ABAD=ac(=adcd)② となり,1つの角を共有する2つの三角形の面積比は,その共有する角をはさむ2辺の積の比と等しくなります。 すなわち、三角比を使った三角形の面積公式も、同じように、 $$\frac{1}{2} \times \text{底辺} \times \text{高さ}$$ をしているだけということですね。
少有人走的路 三角函数超入门 4 钝角三角比 三角形面积
面積公式 三角比
面積公式 三角比- こんにちは、ウチダです。 今日は数学a「図形の性質」で習う 「三角形の内心」 について、性質の証明や基本的な使い方(角の二等分線と比)、座標の求め方や位置ベクトル表示などをわかりやすく解説していきたいと思います。 外心に関する記事と内容がかなり似ているため、こちらの記事5。 三角比を学習する意義 これまでの三角比の現状や先行研究、学習指導要領における目標などから、今 日の三角比を学習する意義は何であるのか。 筆者は高校生が三角比を必修科目「数学I」の中で学ぶ意義について、これ




14 平面及立體圖形 立體圖形的表面積及體積 齊齊溫
三角比を利用して三角形の面積を求めるときには,まず図をかいて,どこの辺や角がわかっているかを確認します。 そして, の公式を使うために,必要な 辺,辺,角 でわかっていないものは何かを調べ,その「準備」をします。 手始めに、高さが同じ三角形の面積比の求め方を考えましょう。 三角形の面積は「(底辺)×(高さ)× 1 2 1 2 」でしたね。 せっかくだから、この面積比の公式をつかってみよう。 つぎの2つの三角形をイメージしてみて。 abcと a'b'c'の辺の長さがそれぞれ、 ab = 3;
三角形の面積を求めるためには 一旦、平行四辺形の面積を求め それを半分にしている。 だから、2で割る必要があるんですね! 忘れないように覚えておきましょう(^^) 三角形の面積を求める問題 それでは、三角形の面積公式を使って問題を解いていきさて、これを理解するためには、数学Ⅰ「図形と計量」の分野で習う A B C = 1 2 b c sin A A B C = 1 2 b c sin A これを知らなくてはなりません。 これを知っている上で解説すると、この三角形の面積の公式より、 A B C A D E = 1 2 A B × A C × sin A 1 2 A D × A E × sin D = A B × A C A D × A E A B C A D E = 1 2 A B × A C × sin A 1 2 A D × A E × sin D = A B × A C A D × A E三角比基礎 >> 三角比(trigonometric ratio)是三角學(Trigonometry)的基本概念之一。簡單嚟講係指一個直角三角形入面兩條邊嘅比。喺初中階段,三角比嘅只會適用及出現於直角三角形上。 在定義三角比函數sin, cos及tan 時,我地要先知道咩係斜邊、鄰邊及對邊。
三角形の内部の点と面積比の公式の証明 (ゼロからわかるベクトル第32回改訂版) 三角形の内部の点と面積比の公式の証明 (ゼロからわかる あくまで三角形の面積の公式は $$(底辺)\times (高さ) \times \frac{1}{2}$$ でありますし、これに対して異論は無いはずです。なので私たちはこれからこの公式を「三角比が出てくる形」に変えてあげることを考えます。では早速やってみましょう。面積の公式 – 三角比の面積公式と計算方法は?いろんな場面での使い方を 様々な平面図形の面積の求め方を一覧にまとめました。図と公式を一緒に覚えましょう!公式の導き方や、面積計算の問題の解き方は、リンク先のページでご覧になれます。



三角形面积公式计算 万图壁纸网




正三角形面積公式證明從三角形的面積談起 Mrsysy
三角形の面積の公式は、 (三角形の面積)=(底辺)×(高さ)÷2 で表せるわけじゃな では、次の三角形を考えてみるかのぉ 上の図の、左の面積Mじゃな この三角形ABDは、底辺はm、高さはh となっているわけじゃ (三角形ABDの面積)= m × h ÷ 2 = M と 三角比による三角形の面積の公式 S=1/2bcsinA の証明と利用 次の公式により,\ 2辺とその間の角の$ {sin}$から三角形の面積を求めることができる {三角形の面積の公式 1/2bcsinA 証明を示す\ 鋭角三角形,\ 直角三角形, 3\ 鈍角三角形に分けて示す必要がある 図の球面三角法(きゅうめんさんかくほう、英 spherical trigonometry )とは、いくつかの大円で囲まれた球面上の図形(球面多角形、とくに球面三角形)の辺や角の三角関数間の関係を扱う球面幾何学の一分野である。 球面上に2点A,Bがあるとき、この2点と球の中心を通る平面で切断したときの断面に




圆的面积公式 圆的面积公式是怎么得到的 52fmz购物网



三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
三角形 ,又稱三邊形,是由三條 線段 順次首尾相連,或不共線的三點兩兩連接,所組成的一個閉合的平面圖形,是最基本和最少邊的 多邊形 。 一般用大寫英語字母 A {\displaystyle A} 、 B {\displaystyle B} 和 C {\displaystyle C} 為三角形的 頂點 標號;用小寫英語字母と、 a'b' = 6;三角形面積公式三角比公式精采文章三角比公式,正三角形邊長公式,直角三角形角度公式,直角三角形公式網路當紅,等腰直角三角形公式,三角形面積算是式:(底*高)/2 這個公式,是任何一種三角形面積都可以算嗎? 我所謂的任何一種三角形是指:等腰三角形、直角三角形等 都可以用(底
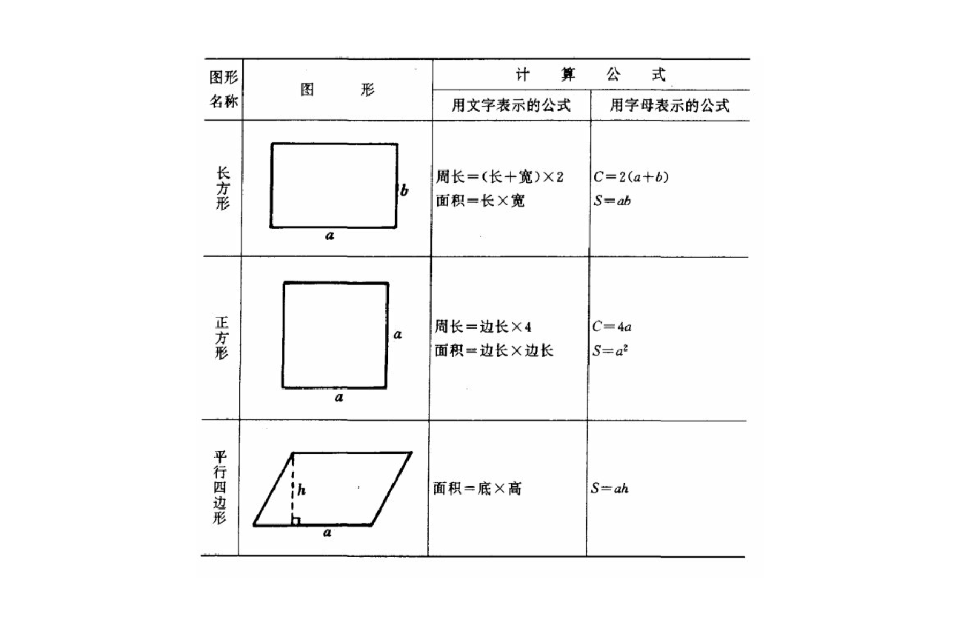



面積公式 常見面積定理 圓公式 扇形公式 圓環面積 三角形公式 海倫公式 坐標公式 中文百科全書




三角函数解三角形知识框架 三角形知识框架图详细 解直角三角形知识框架图
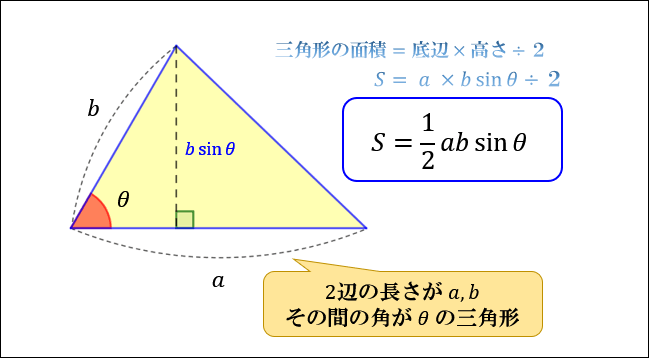
三角形と平行線の線分の比 まずは 三角形と平行線の線分の比の ルールを覚えましょう。 ポイントは ①2つの辺が平行であれば ②どの辺の比の関係が成り立つのか を押さえる というところになります。三角形の面積と三角比 三角形の面積を求める公式は算数の頃から変わりません。 \(\, の面積=(\,底辺\,)\times (\,高さ\,)\div 2\,\) これに正弦を加えると三角比を用いた三角形の面積になります。 正弦定理・余弦定理に+αして知っておきたいのが、三角形の面積を求める公式です。 面積をSとして、S=absinθ/2 三角形の面積は『底辺×高さ×1/2』 で求まりますが、(これは小学校の算数
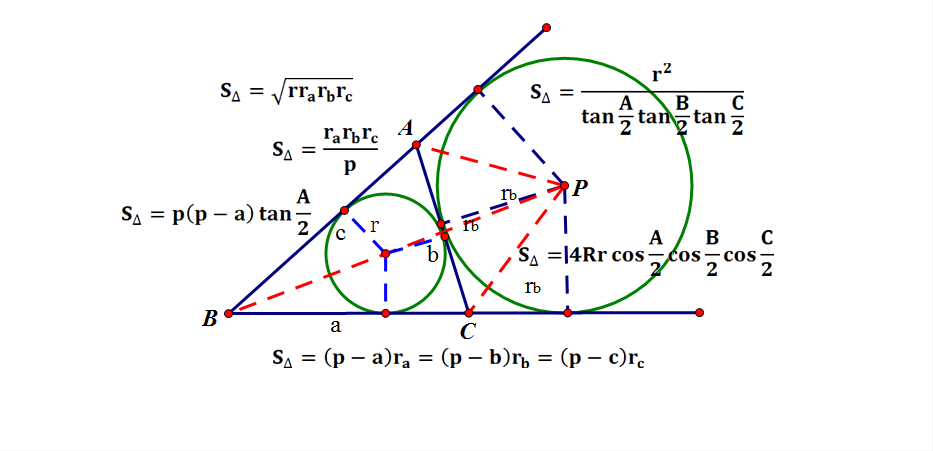



三角形的面积公式二叙 知乎




三角函数 维基百科 自由的百科全书
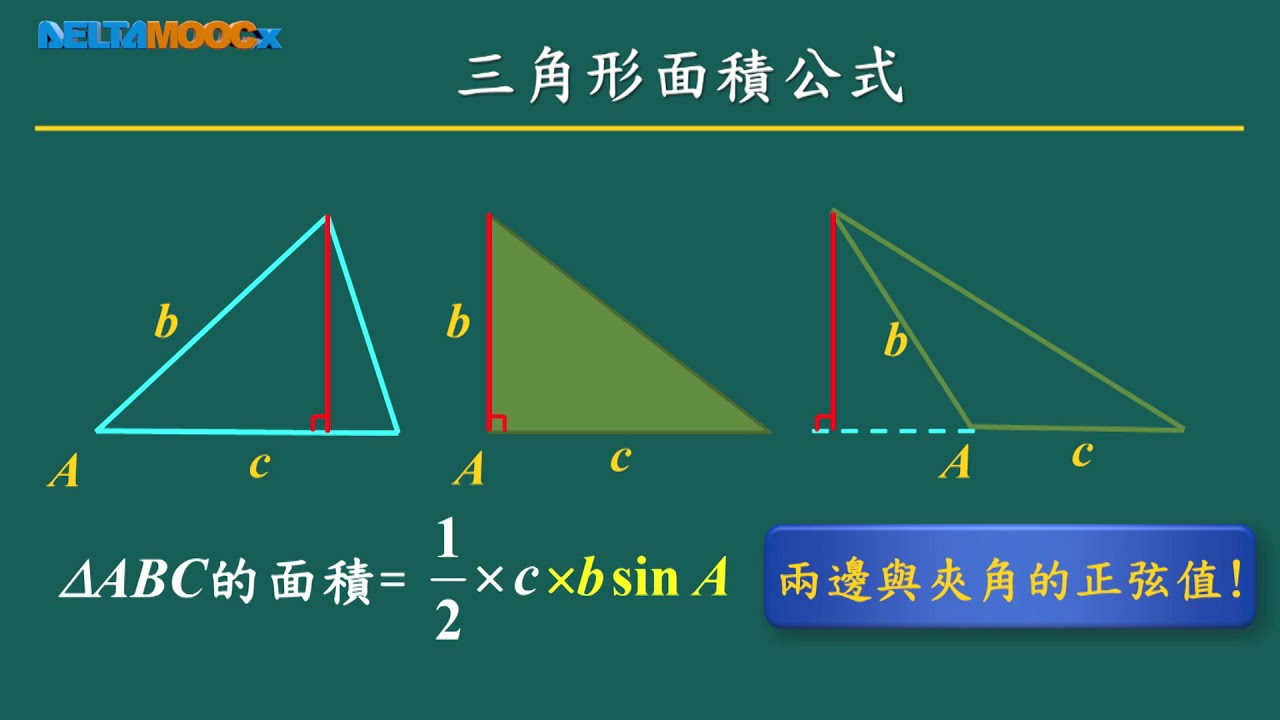
すべての三角形について、 ・ 面積= (1/2)×「ある辺の長さ」×「別の辺の長さ」×「その間の角の sin」 によって求まる ・この公式は鈍角三角形でも使える 授業動画・問題集・姿勢チェックアプリ(完全無料! ) iOS版 無料アプリ Android版 無料アプリ相似の面積比を求める問題をイチからやってみよう! 相似な図形 中3相似中点連結定理、三等分の三角形求め方を問題解説!三角形の3辺の長さのみを用いて,直接三角比を用いないへロンの公式を導きます。 三角比を使った三角形の面積の公式は, 三角比の関係から, なので, ここで, より なので, また, とおくと, 同様にして, , なので, (へロンの公式) この




4种方法来计算三角形面积




14 平面及立體圖形 立體圖形的表面積及體積 齊齊溫
Sinを用いる三角形の面積公式 証明 sinを用いた面積公式の証明をしておきましょう。 三角形ABCにおいて、角Cから辺ABに垂線を引き、垂線と辺ABの交点をHとする。 すると ACHができる。 なので、 三角形の面積は 「底辺×高さ÷2」 でしたね。 したがって長さを測るものさしが1つあれば、三角形の面積をサクッと求められるのです(図3)。 たとえば、三角形の3つの辺が5mと3mと4mなら、 $s=(534)÷2=6$ $T=\sqrt{6(65)(63)(64)}=\sqrt{6×1×3×2}=\sqrt{36}=6$ この三角形の面積は6m 2 となります。三角形の面積を求めるには、 「(底辺)×(高さ)×1/2」 。 ただ、「高さ」が分かっていないんだね。 でも、この「高さ」って、三角比を使って表すことができるよ。 そう、 「(高さ)=(斜辺)×sin」 だよね。 よってポイントの図の例では、 「(高さ)=b×sinA」 として面積を表しているんだ。 POINT こうして、三角比を使って、面積を求めることができるん




三角形知道两边求面积 三角形已知两边求面积公式 三人行教育网 Www 3rxing Org




2 3正弦餘弦定理
中3で学習する「三平方の定理」の中でも、これは応用問題です。例えば、こんな問題です。問題 上の図で、AB=、BC=21、CA=13です。 ABCの面積を求めなさい。まずは、三平方の定理までしか学習していない中3として、この問題をどう解くか考えてみま,セギ英数教室 角木優子 の




弧長公式三角函數三角函數 Thomblake




三角形的面积怎么算小学




高中數學 三角函數 數乙 弧長與扇形面積公式i 曾政清 Youtube



高中数学 三角形与三角函数最全知识点笔记总结 重难点




Sin Cos Tan公式sin Yzkgo



圆面积公式大全 三角形面积计算公式大全及练习题 尚书坊



三角函数面积公式大全 初三网



三角函数 玄数
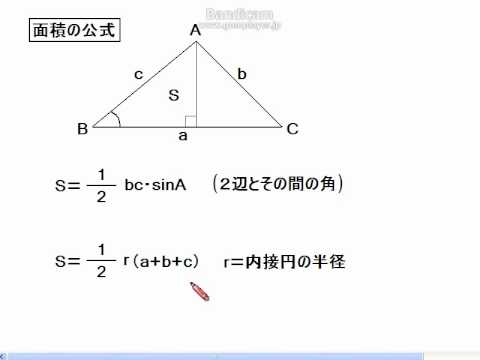



いちちの数学 三角比 面積の公式 Youtube




三角比1 3面積公式與正餘弦定理習作這題怎麼算 Clear




扇形面积公式弧度制极坐标三种3个推导过程 计算机器在线计算




三角形面積公式 兩邊一夾角 Youtube



三角形面积公式 直角等腰三角形面积公式 站长之家 查询网




高中數學必修四 三角函數突破點 二 弧度制及其應用 每日頭條




三角函数所有公式及性质下载 Word模板 爱问共享资料




高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト



數學 高二上三角函數公式 小編過路君子




單元12 三角比的性質




三角形 21 直角三角形面積的基本計算題 Youtube



余弦定理求三角形面积公式 高考辅导网




高中數學三角函數公式匯總 沒有比這更全的了 趕緊拿回去 趣讀




高二高中數學的 高二數學 三角形面積公式3 6 充實版 筆記 Clear




正弦定理與面積公式的應用 重點精析 疑難點撥 第2講 每日頭條




三角形的面积公式小学




360影视 影视搜索



高中數學 三角函數 正弦定理與餘弦定理 1 三角形面積公式 吳汀菱 Youtube




れん 公務員 V Twitter 数的処理の図形問題でこの面積の公式知ってるとめっちゃ便利です 裏ワザみたいなもので 引っ掛けとか関係なく解けてしまいます これに加えて余弦定理と三角比の相互関係知ってると図形問題はほとんど片付きます



初中數學三角函數公式彙總 收藏起來學習 楠木軒




数学 三角比 Sin Cos Tanの面積公式と覚え方 理系ラボ




學測數學 不用再怕 三角函數相關公式一把抓 Clear筆記共享 學生愛用app 痞客邦



三角学 维基百科 自由的百科全书



1



余弦定理求三角形面积公式 高三网



三角 Geogebra




高中數學必修四 三角函數突破點 二 弧度制及其應用 每日頭條



Blog Archives 我的m讚



1




三角函數公式總結 和差化積 積化和差 二倍角 半角 每日頭條
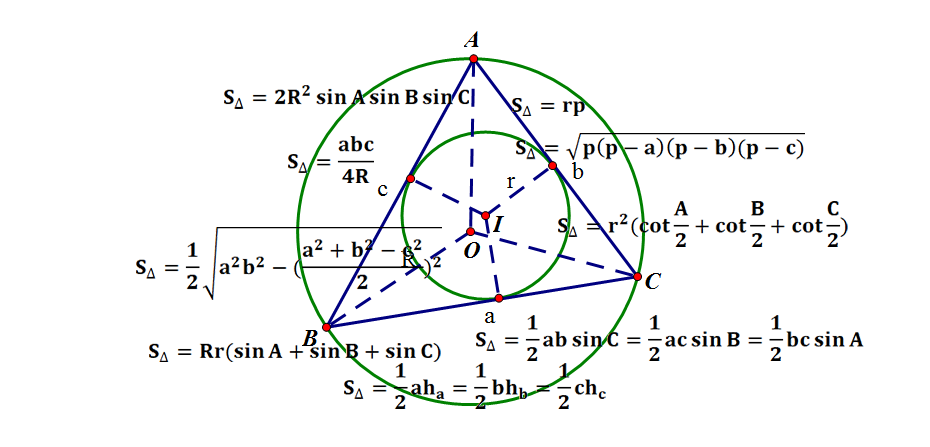



从三角形的面积公式谈起 知乎
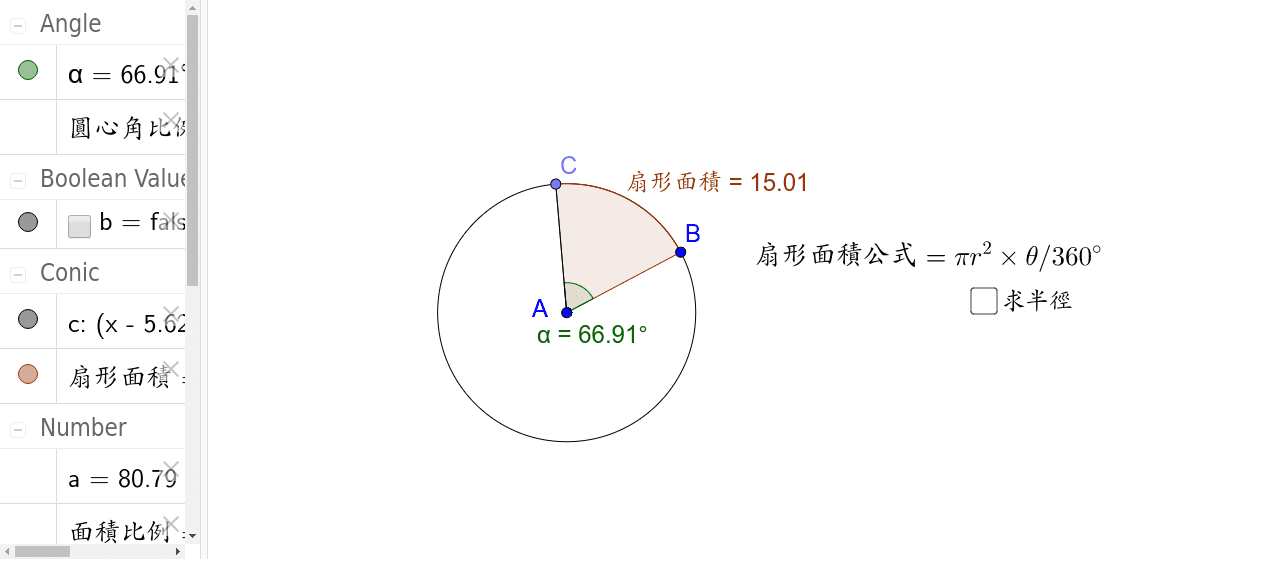



扇形面積公式2 Geogebra




高中數學 三角函數 數乙 弧長與扇形面積公式ii 曾政清 Youtube
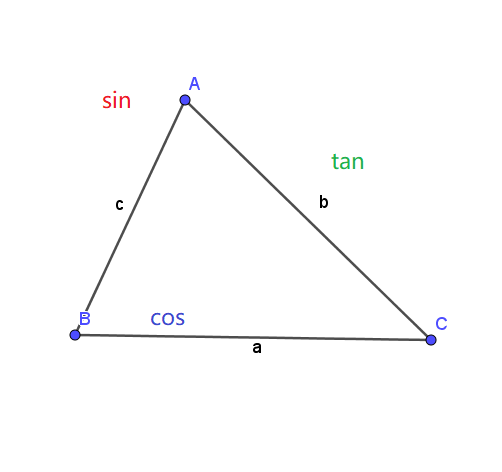



三角形中三角比的特殊公式 知乎




一道面積比公式的另證 的回響 用三角形的a S A 面積公式
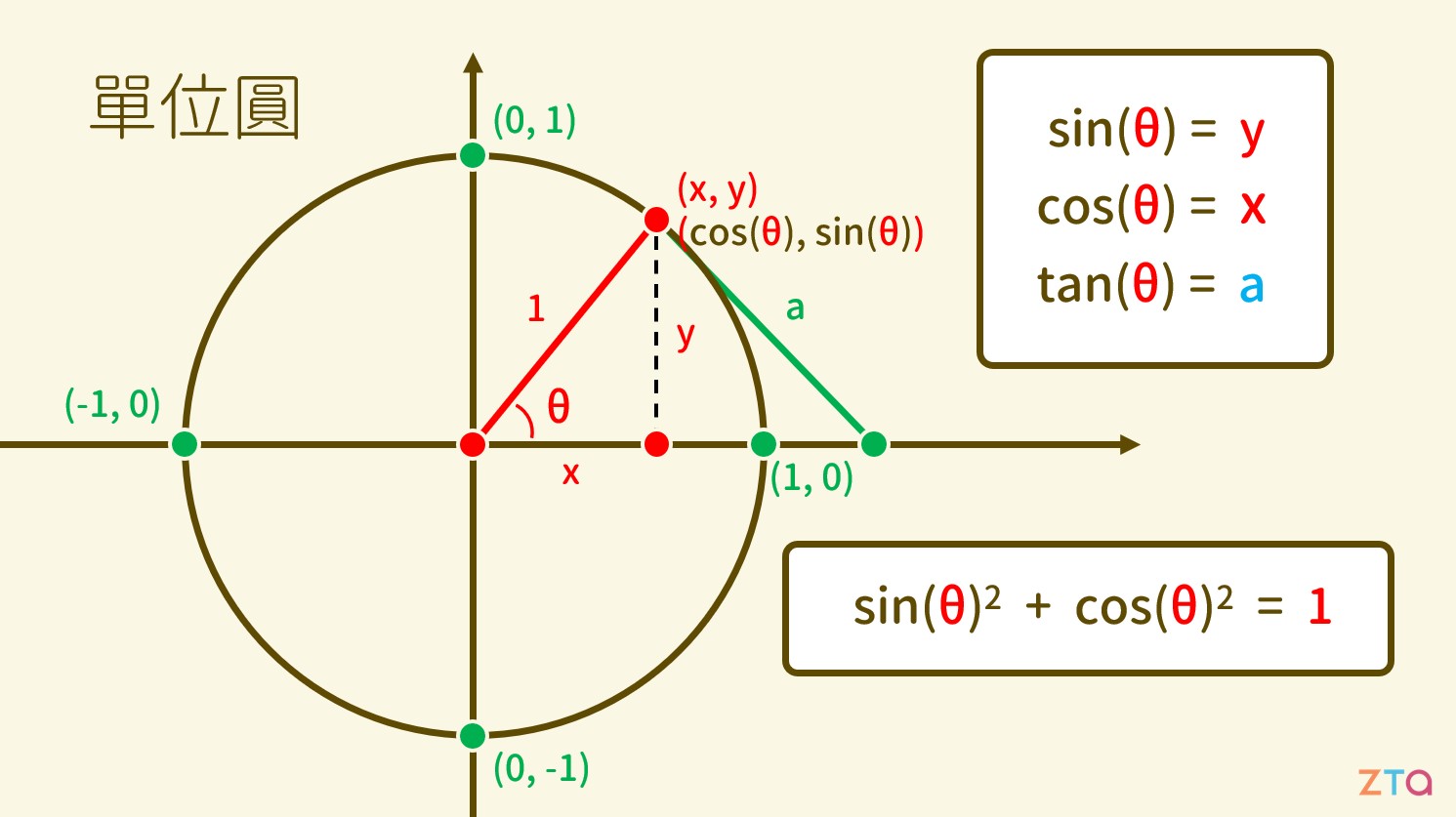



三角函數公式整理 學呀 基礎數學 數學 Sin Cos Tan 單位圓




解三角形知识点归纳 附三角函数公式 Docx 三九文库网




高二高中數學的三角函數公式整理筆記 Clear



Q Tbn And9gcr7w5872uyvmvig8vf1xeyoxmjhhoh Safltyblfewvm9f Tlta Usqp Cau




三角比公式整理



三角形正弦余弦定理 搜狗图片搜索



數學 高二上三角函數公式 小編過路君子



Blog Archives 我的m讚



少有人走的路 三角函数超入门 4 钝角三角比 三角形面积



梯形面积公式换算 梯形形面积计算公式梯形形的面积公式三角形梯形面积公式 尚书坊
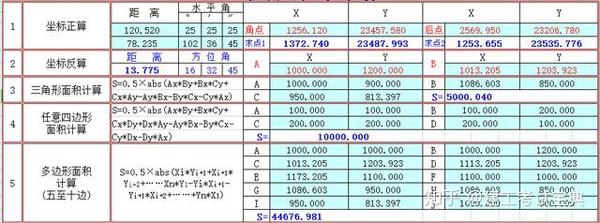



Excel函数公式大全 直接套用 计算速度计算器都比不上 快收藏 面积函数表格 双偶网



少有人走的路 三角函数超入门 4 钝角三角比 三角形面积




三角比を使って三角形の面積を求める方法 数学i By Okボーイ マナペディア




3种方法来求三角形的高



扇形的面积公式 哔哩哔哩 つロ干杯 Bilibili



少有人走的路 三角函数超入门 4 钝角三角比 三角形面积
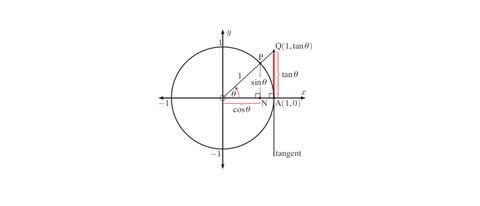



数 你好看 任意角三角函数与诱导公式 知乎



Blog Archives 我的m讚
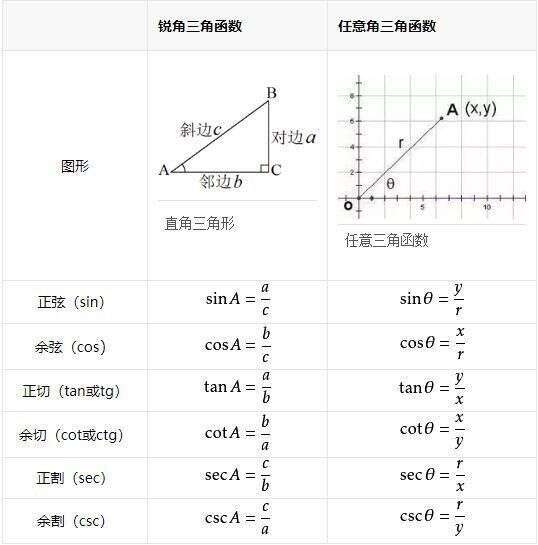



初中數學三角函數公式彙總 收藏起來學習 楠木軒




高校数 三角比 三角形の面積の公式 オンライン無料塾 ターンナップ Youtube




三角形的几个面积公式都是什么时候发现的 网易订阅



1
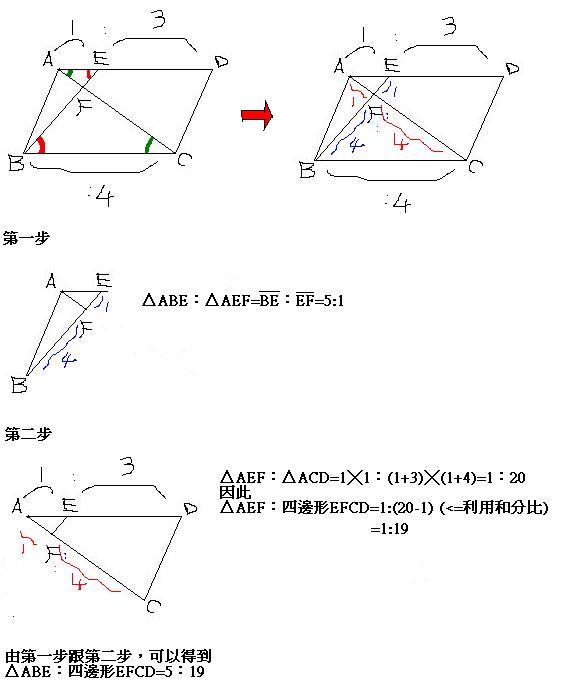



例題 三角函數 三角形面積公式 Iii 平面坐標與向量 高中的數學 Math Pro 數學補給站




玩轉兩弦定理 看如何解三角形 每日頭條



三角形和圆形面积公式 搜狗图片搜索



三角函数公式 快懂百科




學測數學 不用再怕 三角函數相關公式一把抓 Clear筆記共享 學生愛用app 痞客邦




高二高中數學的 高二數學 三角形面積公式3 6 充實版 筆記 Clear




三角形面積公式sin 三角形面積公式 Duph




三角形の面積 三角比 Geogebra
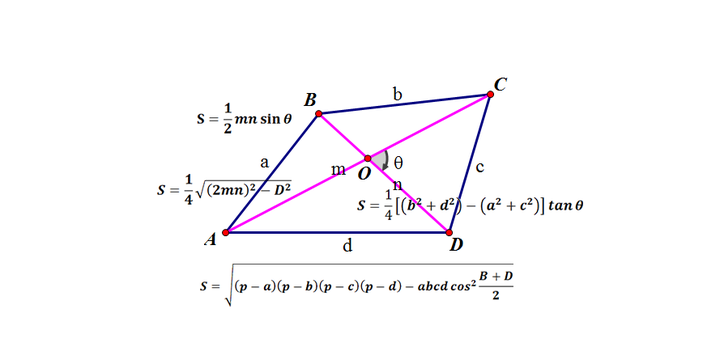



四边形的面积公式 知乎




高二高中數學的數學 三角函數 3 筆記 Clear
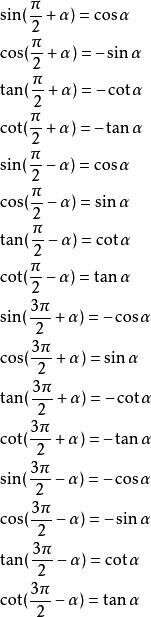



初中数学三角函数公式汇总 收藏起来学习 楠木轩



四边形面积公式 面积最大值问题 哔哩哔哩 つロ干杯 Bilibili




高二高中數學的 高二數學 三角形面積公式3 6 充實版 筆記 Clear




高校数 三角比 三角形の面積 3辺の長さから オンライン無料塾 ターンナップ Youtube



数理之路 三角形面积公式以及三角函数正弦和角公式 腾讯新闻




高校数学 三角比による三角形の面積の公式 S 1 2bcsina の証明と利用 受験の月



数理之路 三角形面积公式以及三角函数正弦和角公式 腾讯新闻




高二高中數學的 高二數學 三角形面積公式3 6 充實版 筆記 Clear



三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典



數學 高二上三角函數公式 小編過路君子




學測數學 不用再怕 三角函數相關公式一把抓 Clear筆記共享 學生愛用app 痞客邦




高中數學必修四 三角函數突破點 二 弧度制及其應用 每日頭條



扇形圆心角公式 万图壁纸网




三角形の面積の三角比を用いた公式 数学の偏差値を上げて合格を目指す




學測數學 不用再怕 三角函數相關公式一把抓 Clear筆記共享 學生愛用app 痞客邦



三角形公式 搜狗图片搜索
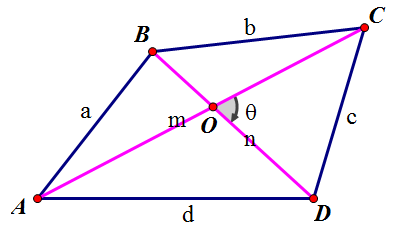



四边形的面积公式 知乎



0 件のコメント:
コメントを投稿